quantum wave

양자 컴퓨팅 분야에서 우리가 가장 크게 기대하는 목표는 단연코 양자 우위와 양자 이득일 것입니다. 양자 우위란, 특정 문제를 고전 컴퓨터로는 사실상 풀 수 없지만 양자 컴퓨터라면 해결할 수 있음을 뜻합니다. 반면, 양자 이득은 양자 알고리즘이 실제 환경에서 고전 알고리즘보다 월등히 우수한 성능을 보일 때 사용되는 용어입니다. 두 개념 모두 고전 컴퓨터보다 훨씬 빠른 속도로 문제를 해결하거나, 기존에는 접근하기조차 어려웠던 영역을 탐구할 수 있으리라는 기대를 반영합니다. 하지만 과연 현재의 양자 컴퓨팅 기술이 이러한 기대를 완벽히 충족할 수 있을까요?
이 물음에 쉽사리 ‘그렇다’고 대답하기는 어렵습니다. 가장 큰 이유는 이론적으로 제시된 양자 알고리즘과 실제 하드웨어 기술 사이에 여전히 큰 간극이 존재하기 때문입니다. 예를 들어, 쇼어 알고리즘은 양자 푸리에 변환을 이용해 정수를 매우 빠르게 소인수분해함으로써, 이론적으로는 고전 알고리즘보다 훨씬 빠르게 RSA 암호를 깨뜨릴 수 있을 가능성을 제시합니다. 그러나 이를 실제 장치에서 구현하려면 오래 유지되는 결맞음 시간이 확보된 큐비트가 필요합니다. 현재 기술 수준의 물리적 큐비트만으로는 이 조건을 충족하기가 쉽지 않으며, 오류 정정 코드를 사용해 논리적 큐비트를 만든다고 해도, 그에 필요한 물리적 큐비트의 수는 현재 가용한 양자 자원을 훨씬 초과합니다.
이처럼 기술적 제약이 분명하므로, 연구자들은 지금 당장 활용 가능한 하드웨어에서도 양자 우위를 발휘할 수 있는 방법을 모색하게 되었습니다. 그 대안으로 주목받은 것이 바로 양자 샘플링 문제입니다. (가우시안) 보손 샘플링, 랜덤 회로 샘플링 등이 대표적 예 입니다.1 특히 가우시안 보손 샘플링은 몇몇 실험에서 고전적인 계산 능력을 넘어서는 결과를 냈다고 평가되고, 최근 구글이 추진한 윌로우 프로젝트는 랜덤 회로 샘플링을 대규모로 구현해 고전 컴퓨터가 풀기 어려운 영역에서 양자 샘플링을 성공적으로 수행했다는 의의를 남겼습니다.
그렇지만 현실 세계에서 중요한 계산 문제들은 대부분 특정 수학적·물리적 구조를 가지고 있고 이를 활용해 고전 컴퓨터로도 어느 정도 근사적인 해답을 구할 수 있습니다. 반면 양자 샘플링은 이런 구조를 의도적으로 배제하여 고전 컴퓨터가 접근조차 하기 어렵도록 설계된 특수한 형태의 문제들입니다. 다시 말해, 큰 규모의 양자 샘플링 구현은 양자정보학적으로 중요한 이정표라는 데에는 이견이 없지만, 실제 산업이나 연구 현장에서 광범위하게 쓰일 수 있을지는 불명확합니다. 더불어, 기존의 큐비트 기반 양자 컴퓨팅 방식이 가진 비효율성도 고려해야 합니다. 예를 들어, 양자 오류 정정 코드는2 물리적 큐비트 여러 개를 묶어 논리적 큐비트로 구성되는데, 이때 필요한 물리적 큐비트의 수가 워낙 많아 현실적으로 구현하려면 많은 난관을 극복해야 합니다. 또한, 보손 시스템처럼 차원이 사실상 무한대에 가까운 양자 시스템을 큐비트로만 표현하려고 하면 많은 자원을 소모하는 비효율적인 상황이 발생합니다. 근사 과정을 통해 보손 시스템을 큐비트로 변환한다고 해도, 그 상태와 게이트를 제대로 표현하기 위해서는 여전히 막대한 양자 자원이 필요합니다.
그렇다면 제한된 양자 리소스를 효율적으로 활용하면서, 고전 컴퓨팅과 비교해 우수한 능력을 발휘할 수 있는 또 다른 방법은 무엇일까요? 최근 주목받고 있는 아이디어 중 하나는, 기존의 (큐비트 기반) 양자 컴퓨팅에 더해 보손 모드를 함께 사용하는 연속-이산(Continuous-Variable-Discrete-Variable) 하이브리드 양자 프로세서를 도입하는 것입니다. 이 글에서는 바로 그 연속-이산 양자 프로세서의 개념과 가능성에 대해 소개합니다. 이어지는 내용은 미국 예일대학의 Steven Girvin 교수가 발표한 리뷰 논문 [Liu2024]을 상당 부분 참고하여 작성했음을 밝혀둡니다.

하이브리드 양자 시스템

대부분의 양자 컴퓨팅 연구는 이산 변수인 큐비트를 중심으로 진행되어 왔습니다. 반면, 보손 모드(조화 진동자)는 무수히 많은 상태를 가질 수 있으며, 특히 운동량이나 위치를 이용해 표현할 수 있어 연속 변수로 분류됩니다. 이 두 요소를 결합한 하이브리드 양자 진동자-큐비트 시스템(또는 하이브리드 연속-이산 시스템)은 큐비트와 보손 모드를 함께 활용해 양자 정보를 저장하고 조작하는 방식을 제공합니다.
지난 20년 동안 다양한 양자 컴퓨터 하드웨어에서 하이브리드 장치 아키텍처가 연구되었고, 그 과정에서 양자 제어와 양자 오류 수정에 대한 상당한 이론적·실험적 진전이 이루어졌습니다. 보손 모드는 큐비트들 간의 얽힘을 생성하는 매개체로 활용될 뿐만 아니라, 오류 정정 코드를 구성하거나 스핀-보손 간 상호작용을 시뮬레이션하는 중요한 요소로도 주목받고 있습니다. 이렇게 탄생한 하이브리드 진동자-큐비트 시스템은 기존의 큐비트 기반 접근법과는 전혀 다른 패러다임을 제시하며, 전통적 방법보다 유리한 장점을 제공할 수 있습니다.
먼저, 보손 모드를 포함한 양자 현상을 더 정밀하게 시뮬레이션할 수 있어 복잡한 물리적 시스템을 한층 효과적으로 분석할 수 있습니다. 둘째, 연속 변수를 활용해 진동자의 무한 차원 상태 공간을 이용하면 자원 효율적인 양자 오류 수정을 수행할 수 있습니다. 하이브리드 시스템은 큐비트의 정밀성과 진동자의 견고함을 결합해 더욱 강력한 양자 시뮬레이션과 개선된 오류 수정 기법을 가능케 합니다. 셋째로, 이러한 시스템은 기초적인 연산에서부터 복잡한 양자역학적 시뮬레이션까지 다양한 양자 작업에 적용될 수 있습니다.
이를 종합해보면 하이브리드 연속-이산 시스템은 양자 컴퓨팅의 영역을 넓히고, 높은 정확도와 효율을 제공할 잠재력을 갖추고 있다고 볼 수 있습니다. 특히 연속 변수와 이산 변수가 지닌 장점을 접목하면, 보손 모드를 이용한 복잡한 양자 시뮬레이션과 오류 수정 메커니즘을 더욱 발전시킬 수 있습니다. 또한, 하이브리드 양자 연속-이산 시스템은 현재 양자 컴퓨팅 기술이 직면한 여러 도전 과제를 극복할 강력한 대안으로도 거론되고 있습니다. 이는 큐비트가 선사하는 정밀한 제어 능력과 진동자가 지닌 우수한 오류 수정 잠재력이 어우러져, 보다 효율적이고 유연한 양자 정보 처리를 가능하게 하기 때문입니다.
지금부터 이러한 하이브리드 시스템의 이론적 기초, 실용적 도전 과제, 그리고 잠재적 응용 분야를 차례로 살펴보고자 합니다. 특히 하이브리드 양자 연속-이산 프로세서의 잠재력과 이를 실현하기 위해 해결해야 할 문제들을 살펴보면서, 추상 기계 모델(AMM; Abstract Machine Models)과 명령 세트 아키텍처(ISA; Instruction Set Architectures)3의 필요성을 설명할 것입니다. 이에 더해 마지막으로 하이브리드 시스템의 주요 응용 분야 중 하나로 꼽히는 해밀토니안 시뮬레이션도 함께 논의합니다. 이를 통해 하이브리드 양자 시스템이 어떻게 양자 컴퓨팅의 한계를 확장하고, 새로운 가능성을 열어줄 수 있는지 구체적으로 조망해 보고자 합니다.

하이브리드 연속-이산 시스템의 물리적 메커니즘

이미지 확대보기

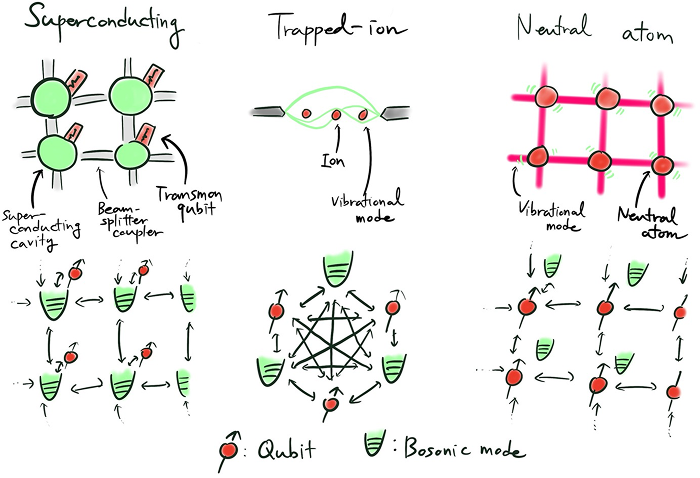
Figure 1. 연속-이산 하이브리드 양자 프로세서: 초전도 회로(좌), 이온 포획(중), 중성원자(우). 구현하는 양자 컴퓨터 하드웨어에 따라 (진동자-큐비트) 하이브리드 시스템의 연결성과 특성이 달라진다.
하이브리드 연속-이산 시스템은 오늘날 다양한 양자 컴퓨터 하드웨어에서 구현되어 왔습니다. 특히 보손 모드를 활용해 큐비트 간 양자 얽힘을 생성하는 연구가 활발히 진행되면서, 보손 모드와 큐비트의 상호작용에 대한 이해가 크게 발전했습니다. 이러한 성과를 바탕으로, 여러 양자 컴퓨터 하드웨어에서 하이브리드 연속-이산 시스템이 이론적·실험적으로 폭넓게 탐구 되고 있습니다. 여기서는 그 대표적인 물리적 구현 사례들을 살펴보겠습니다.
먼저, 초전도 회로를4 이용한 사례입니다. 초전도 마이크로파 공진기(연속 변수)는 개별 초전도 큐비트(이산 변수)와 분산 결합된 형태로 구성되어, 큐비트와 마이크로파 진동자(보손 모드)의 광자 상태에 양자 정보를 저장하고 조작할 수 있습니다. 인접한 마이크로파 공진기는 마이크로파 빔가르개로 연결되어 있어, 약 100 ns의 짧은 시간에 99.9% 수준의 신뢰도로 SWAP 게이트를 수행할 수 있습니다. 이를 통해 큐비트와 진동자 간의 원격 통신과 얽힘이 가능합니다. 또한 각 큐비트는 단일 보손 모드에 연결되어 크로스토크가 최소화되며, 공진기 모드를 연결하는 빔가르개를 마이크로파로 실시간 제어할 수 있어 2차원 하드웨어 전반에서 양자 정보를 빠르고 안정적으로 전파할 수 있습니다. 더 나아가 초전도 아키텍처에서는 광자 수 패리티를 비파괴적으로 측정할 수 있으므로, 오류가 발생하더라도 위치 파악과 수정이 용이하다는 이점이 있습니다.
다음으로, 이온 포획 장치5에서는 이온 배열의 모든 집단 운동 모드(연속 변수)가 각각 이온 스핀 큐비트(이산 변수)와 연결되어 있어, 장거리 연결 뿐 아니라 일대일 연결도 가능하다는 특징이 있습니다. 이는 하나의 전기 퍼텐셜에 포획된 이온에게 매우 높은 유연성과 연결성을 제공하지만, 큐비트 간 혹은 진동자-큐비트 간 상호작용은 진동자의 주파수와 스핀 큐비트 주파수의 선형 조합으로 정해진 레이저 주파수를 통해 이루어집니다. 따라서 하나의 퍼텐셜 안에 더 많은 이온이 포획될수록 이온 간 간격이 좁아져 진동자 모드의 주파수 밀도가 높아지고, 그 결과 크로스토크 위험도 커질 수 있습니다.
마지막으로, 광학 집게 배열의 중성 원자6 시스템에서는 원자 큐비트(이산 변수)가 개별 원자의 운동 모드(연속 변수)와 연결되는 형태로 구성됩니다. 초전도 아키텍처와 마찬가지로 각 큐비트는 단일 운동 모드에만 연결되어 있어 크로스토크가 최소화되며, 빔가르개 대신 인접한 중성 원자 간 리드버그 상호작용을 통해 큐비트 간 연결을 형성합니다. 이처럼 다양한 물리적 시스템에서 구현되는 연속-이산 하이브리드 구조는 양자 정보의 저장과 조작 측면에서 높은 확장성과 신뢰도를 확보할 수 있어, 차세대 양자 프로세서의 실현 가능성을 더욱 앞당길 것으로 기대됩니다.

양자 게이트: 진동자-큐비트 하이브리드 게이트

이처럼 다양한 양자 컴퓨터 하드웨어는 저마다 보손 모드와 큐비트 간의 고유한 연결 구조와 특성을 갖추고 있습니다. 하드웨어마다 구현하기 쉬운 게이트를 활용해 보손 모드와 큐비트의 상태를 조작할 수 있는데, 큐비트 자체를 다루는 방법은 이미 많은 양자 컴퓨팅 플랫폼에서 잘 확립되어 있으므로, 여기서는 진동자-큐비트 간 상호작용을 기반으로 한 하이브리드 게이트, 특히 이를 통해 보손 상태에 작용할 수 있는 게이트들을 중심으로 살펴보겠습니다.
일반적으로 양자 컴퓨터 하드웨어에 존재하는 보손 모드에는 보손 모드만을 대상으로 하는 게이트도 있지만, 실질적으로는 큐비트와의 상호작용을 통해 보손 모드의 상태를 조절하는 경우가 많습니다. 예컨대, 초전도 회로에서는 보손 모드와 큐비트가 분산 상호작용으로 연결되어 있고, 이온 포획 시스템에서는 제인스-커밍스 상호작용 (Jaynes-Cummings interaction)7이 사용됩니다. 이들 상호작용은 보손 모드와 큐비트 간 양자 얽힘을 생성할 뿐 아니라, 보손 게이트를 구현하는 기반이 되기도 합니다. 특히 보손 게이트는 전통적인 양자 광학 시스템에서 사용하는 방식보다 복잡한 연산을 비교적 쉽게 실현할 수 있어, 보손 기반 컴퓨팅의 잠재력을 한층 높여줍니다.

보손 상태에 작용하는 게이트는 크게 가우시안 게이트와 비-가우시안 게이트로 나눌 수 있습니다. 가우시안 게이트는 보손의 바닥상태로부터 시작해 가우시안 형태의 양자 상태를 유지하면서 변환하는 연산을 말합니다. 변위 게이트, 위상공간 회전 게이트, 단일모드 압축 게이트가 대표적이고, 두 모드 빔가르개/압축/합 게이트 역시 여기에 속합니다. 양자 광학에서는 이들을 선형 광학 요소로 구현할 수 있어 선형 게이트라고도 부르며, 큐비트 게이트의 클리포드 게이트에 비유할 수 있습니다. 클리포드 게이트와 선형 게이트 모두 구현이 비교적 용이하지만, 이들만으로는 유니버설(범용) 컴퓨팅을 달성하기 어렵다는 유사성이 있습니다.

반면, 비-가우시안 게이트는 가우시안 함수를 유지하지 않는 연산으로, 선형 광학 요소만으로는 구현이 불가능해 비선형 게이트라고 부르기도 합니다. 예를 들어, 위치 연산자의 세제곱 항을 포함하는 조화 진동자의 해밀토니안에 대한 시간 진화 연산은 가우시안 상태를 유지하지 못하므로 비-가우시안 게이트에 해당합니다. 가우시안 게이트에 비-가우시안 게이트를 조합하면 보손 시스템에서 유니버설 컴퓨팅을 구현할 수 있으나, 전통적인 양자 광학 방식으로는 이를 실현하기가 쉽지 않았습니다.

이때 진동자-큐비트 하이브리드 게이트는 큐비트와 보손 모드 간의 상호작용을 능동적으로 제어함으로써, 비선형 게이트를 비롯한 보다 복잡한 보손 게이트들을 구현할 수 있게 해줍니다. 예컨대 큐비트 파트의 파울리 연산자 교환 관계나, 시스템 고유의 진동자-큐비트 상호작용을 이용해, 조건부로 작동하는 패리티 게이트·위상공간 회전 게이트·변위 게이트·압축 게이트 등을 구축할 수 있습니다. 더 나아가 숫자 기저(number basis)에 따라 큐비트 회전 변환이나 위상 변환을 달리 적용하는 고차원적 비선형 게이트도 실현 가능합니다. 예를 들어 조건부 변위 게이트를 활용하면 단일 게이트만으로 캣(Cat) 상태를 만들 수 있고, 복잡한 보손 해밀토니안의 시간 진화를 모사하는 연산자들도 구현할 수 있습니다.

이처럼, 하이브리드 게이트 전략을 통해 보손 상태의 제어 범위가 대폭 확장되면서, 보손 모드를 활용한 범용 양자 컴퓨팅이 한층 현실에 가까워지고 있습니다. 이러한 흐름은 향후 양자 하드웨어와 소프트웨어 전반에 중요한 패러다임 변화를 가져올 것으로 기대됩니다.

하이브리드 프로세서에 맞춘 AMM 및 ISA의 개발

추상 기계 모델(AMM)은 실제 하드웨어나 구현 세부사항을 배제한 채, 계산 과정을 수학적이고 개념적으로 표현하는 틀로서 알고리즘 설계와 시스템 복잡도를 분리하여 이해할 수 있게 해줍니다. 반면, 명령 세트 아키텍처(ISA)는 프로세서가 이해하고 실행할 수 있는 기계어 명령들의 집합과 그 형식을 정의함으로써, 소프트웨어와 하드웨어가 소통하는 핵심 인터페이스를 제공합니다.
큐비트 기반 양자 컴퓨터와 마찬가지로, 하이브리드 진동자-큐비트 시스템을 본격적으로 구현하려면 단순히 하드웨어만 활용하는 수준을 넘어, 연속 변수와 이산 변수 기술을 통합하기 위한 새로운 양자 오류 수정 전략과 정교한 양자 작업을 지원할 수 있는 견고한 AMM이 필수적입니다. 나아가 이 프로세서를 프로그래밍하고, 그 계산 능력을 제대로 평가하기 위해서는 기존 방식과는 다른 혁신적인 하드웨어·소프트웨어 공동 설계가 필요합니다. 또한, 하이브리드 양자 프로세서의 잠재력을 극대화하려면, 하드웨어에서 수행 가능한 연산을 체계적으로 정의하는 AMM과 ISA를 함께 구축하는 일이 중요합니다. 특히 연속 변수와 이산 변수라는 상이한 양자 시스템을 동시에 다루는 하이브리드 환경에서 보편적 제어를 실현할 수 있는 ISA를 설계하는 것은 매우 중요한 과제지만 기술적로 쉽지 않습니다. 이 아키텍처가 제대로 정립된다면, 하이브리드 시스템의 계산 능력을 정량화하는 것은 물론, 알고리즘을 효과적으로 설계하여 전반적인 효율성과 결함허용오차를 향상시키는 데에도 크게 기여할 것입니다.

이미지 확대보기

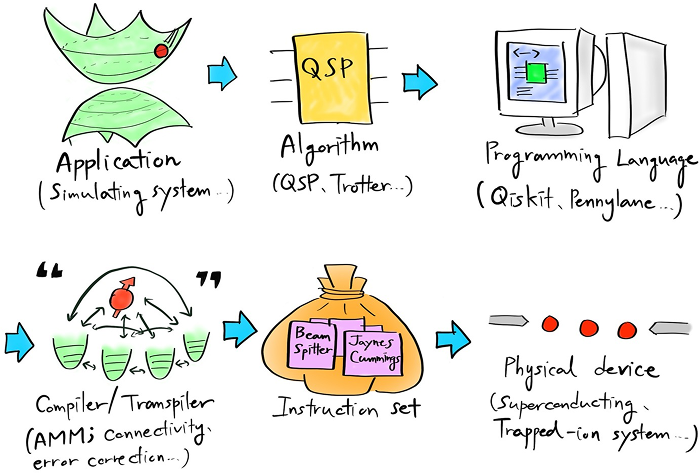
Figure 2. 양자컴퓨팅 아키텍처와 작동순서 예시

위의 그림은 이러한 하이브리드 진동자-큐비트 시스템 아키텍처를 개략적으로 보여줍니다. 예를 들어, 어떤 물리 시스템에서 페르미온과 보손 입자가 함께 등장하는 상황을 시뮬레이션하려 한다면, 먼저 이를 구현할 알고리즘이 필요하고, 알고리즘을 프로그래밍 언어로 표현할 수 있어야 합니다. 이후 작성된 프로그램을 실행하려면, 이에 맞는 AMM과 ISA가 필수적으로 요구됩니다. 이후 컴파일 과정을 거쳐 하드웨어에서 요구하는 네이티브 양자 회로를 생성하고, 최종적으로 시뮬레이션을 실행하게 됩니다.
하이브리드 진동자-큐비트 하드웨어 계층은 크게 세 가지 다른 AMM을 제시할 수 있습니다. 첫 번째 모델은 큐비트 중심으로, 양자 정보가 큐비트에 저장·조작되며, 진동자 모드는 큐비트 간 장거리 양자 통신 버스로서 간접적으로만 활용됩니다. 두 번째 모델은 진동자 중심으로, 공진기 내 광자 상태에 보손 오류 정정 코드를 적용해 양자 정보를 저장·조작하고, 큐비트는 광자 상태를 제어하기 위한 비선형 보조 요소로 활용됩니다. 마지막으로 사용자가 하이브리드 계산이나 보손·스핀을 모두 포함하는 물리 모델 시뮬레이션을 하고자 할 때, 하이브리드 진동자-큐비트 하드웨어를 직접 활용하는 모델이 있습니다. 이 세 가지 AMM은 각각 소프트웨어 스택의 컴파일러 계층에 다른 기능을 노출하며, 그에 따라 별도의 ISA가 필요해 집니다.
이후에는 이러한 시스템을 구체적이고 효과적으로 실행하기 위한 컴파일 방법을 고안해, 이론적·실험적 효율을 최대화해야 합니다. 마지막으로, 하이브리드 양자 프로세서가 실제로 활용될 수 있는 구체적인 사용 사례를 발굴하고 검증하는 과정이 필요합니다. 이러한 모든 과정을 종합적으로 수행함으로써, 하이브리드 양자 시스템의 강점을 최대한 이끌어낼 수 있을 것입니다.

양자 하이브리드 시스템의 컴파일 기법

하이브리드 시스템에서 양자 알고리즘을 실제 하드웨어 지침으로 변환(컴파일)하는 기법은, 하이브리드 시스템 내 양자 신호 처리를 구현하는 방법을 말합니다. 일반적으로 컴파일은 한 프로그래밍 언어를 다른 프로그래밍 언어로 변환하는 과정을 말하고, 트랜스파일링은 고수준 ISA를 큐비트 연결 정보를 인식하는 저수준 하드웨어 명령어로 변환하는 과정을 뜻합니다. 여기서는 이 둘을 구분하지 않고, 모두 통칭해 ‘컴파일’이라고 하겠습니다.
양자 프로그래밍 언어 자체가 아직 초기 단계이며, 특히 보손 프로그래밍 언어와 관련해서는 고전 컴퓨터의 컴파일 방식 수준으로 확립된 체계가 거의 없는 실정입니다. 하이브리드 진동자-큐비트 알고리즘을 컴파일하는 핵심은, 다중 진동자-큐비트 유니터리 연산자를 보손 ISA 중 하나로 얼마나 효율적으로 분해할 수 있는가에 달려 있습니다. 하이브리드 연속-이산 양자 컴퓨터에서 일반적인 알고리즘 작업은 측정과 피드포워드가 교차되는 여러 유니터리 작업으로 구성되며, 측정 결과에 따라 새로운 유니터리를 생성합니다. 또한 하이브리드 구조에는 빔가르개와 같은 네이티브 진동자-멀티큐비트 유니터리가 포함되어 있어, 이를 컴파일 과정에서 기본 요소로 활용할 수 있습니다.
그러나 알고리즘이 복잡해 질수록, 이러한 컴파일 규칙을 하나하나 추적하는 일은 점점 어려워지고 비효율적으로 변합니다. 이 때문에 현대 컴파일러에서는 좋은 회로를 찾기 위해 수치 최적화 알고리즘을 도입하고 있습니다. 일부 초전도 회로 하드웨어 플랫폼에서는 트랜스몬 큐비트들이 서로 직접적으로 근접 연결되어 있지만, 초전도 회로 큐비트/공진기 구조는 크로스토크 문제를 피하기 위해 이러한 직접 연결을 의도적으로 제한합니다. 대신 다중 큐비트 결합 게이트를 공동체로 사용하는 분석적 컴파일 전략을 통해, 고수준 알고리즘이 큐비트와 진동자를 동등하게 취급하면서도 빠르고 신뢰도 높은 SWAP 게이트를 활용해 논리적으로 모두 연결할 수 있게 합니다.

응용 가능성: 해밀토니안 시뮬레이션

이제 해밀토니안 시뮬레이션을 중심으로, 하이브리드 진동자-큐비트 시스템을 통해 기대할 수 있는 응용 가능성들을 소개하고자 합니다. 해밀토니안 시뮬레이션은 주어진 양자 시스템의 상태와 시간이 흐름에 따라 변화를 모사하여, 양자 시스템을 이해하는 데 필수적인 역할을 합니다. 하지만 고전 컴퓨터로는 양자 시스템의 규모가 커질수록 계산량과 저장 공간이 지수적으로 늘어나기 때문에, 정확한 모사가 점점 어려워집니다.
이로 인해 다양한 근사적 기법들이 개발되었지만, 이들 역시 한계를 지닙니다. 예를 들어 평균장 이론(Mean-Field Theory)나 준고전 근사법(Semiclassical Approximation)은 입자 간 상관관계를 제대로 포착하지 못합니다. 결합 클러스터 이론(Coupled-Cluster Theory)와 텐서 네트워크(Tensor network) 기반 기법은 힐베르트 공간(Hilbert space)을 제한적으로만 취급하기 때문에, 강한 상관관계가 존재하는 시스템에서는 부정확한 결과를 초래할 수 있습니다. 또한 양자몬테카를로 (Quantum Monte Carlo) 같은 샘플링 기반 방법들은 부호 문제나 위상 문제 등으로 인해 활용에 제약이 따릅니다.

이미지 확대보기

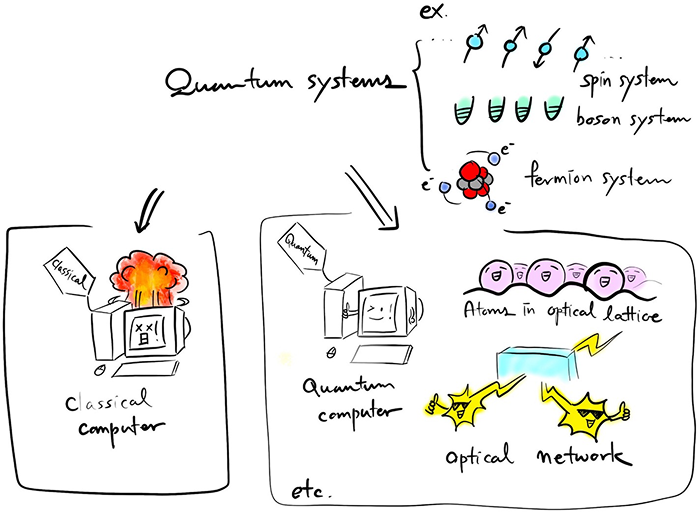
Figure 3.  양자시스템을 클래식컴퓨터에서 시뮬레이션 할 경우, 메모리 및 실행시간에 대해 부하가 걸릴 수 있지만, 양자컴퓨터의 경우엔 보다 효율적으로 처리할 수 있다.

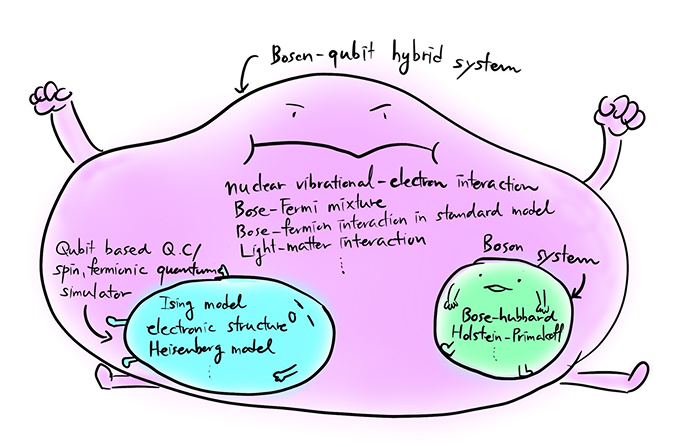
이에 대한 대안으로, 양자 컴퓨터나 제어 가능한 양자 시스템을 활용한 해밀토니안 시뮬레이션이 제안되어 왔고, 실제 실험도 진행되어 왔습니다. 예를 들어, 양자 컴퓨터나 광학 격자를 이용한 양자 시뮬레이터에서는 스핀 혹은 페르미온 모델에 대한 시뮬레이션이, 광학 네트워크에서는 보손 모델에 대한 시뮬레이션이 각각 시도되었습니다. 그러나 지금까지 이루어진 해밀토니안 시뮬레이션은 대체로 하나의 종류(스핀, 보손, 혹은 페르미온)만을 다루었으며, 분자양자동역학에서 나타나는 핵의 진동과 전자 간 상호작용이 결합된 문제나, 표준 모델에서의 보손-페르미온 상호작용처럼 두 종류 이상의 해밀토니안을 포함하는 경우, 특히 보손이 포함된 다종 해밀토니안에 대한 시뮬레이션 연구는 활발히 진행되지 못했습니다. 이는 하나의 양자 시스템이 주로 한 가지 자유도(예: 광학 네트워크는 보손 자유도만)를 갖고 있었기 때문이며, 이러한 한계를 극복하기 위해 여러 종류의 자유도를 모두 포함하는 양자 플랫폼의 필요성이 대두되었습니다.
큐비트 기반 양자 컴퓨터의 경우, 큐비트를 활용해 다양한 시스템(스핀, 페르미온, 보손 등)을 모사하고 해밀토니안 시뮬레이션을 수행하려는 시도가 많았습니다. 그러나 특히 큐비트로 보손을 모사하려 할 때, 보손 상태 자체는 근사적으로 구현하기가 비교적 쉽지만, 보손의 연산자를 구현하기 위해서는 너무 많은 큐비트 게이트가 필요해 효율적이지 못하다는 단점이 있습니다.
보손 시스템을 직접 사용하는 경우를 살펴보면, 더 복잡한 보손 해밀토니안을 시뮬레이션하기 위해서는 비-가우시안 연산이 필수적입니다. 그러나 주로 보손을 모사하는 광학 네트워크에서 실제 환경에서 비-가우시안 연산을 구현하는 일은 쉽지 않습니다. 또한 보손 시스템으로 큐비트 시스템을 모사하려 할 때 역시, 큐비트 연산자를 효율적으로 구현하기 어렵다는 단점이 존재합니다.
반면, 진동자-큐비트 하이브리드 시스템은 보손과 큐비트를 동시에 가지는 구조이므로, 기존에 큐비트만 이용해 해밀토니안 시뮬레이션을 하던 방식과 보손만 이용하던 방식을 통합할 수 있습니다. 나아가 보손과 큐비트가 결합된 다종 해밀토니안 시뮬레이션까지 효율적으로 수행할 수 있게 해줍니다. 예를 들어, 이온 포획 시스템에서는 진동자-큐비트 하이브리드 게이트를 이용해 진동 모드로 분자의 진동 구조를 모사하거나, 핵 진동 모드와 전자의 상호작용으로 인한 원뿔교차로 (Conical Intersection)8 같은 양자 현상을 진동 모드와 큐비트를 사용해 실험한 사례가 보고되었습니다. 또한 진동 모드를 스핀 시스템과 에너지를 교환하는 환경으로 설정해 열린 양자 시스템을 시뮬레이션한 실험도 존재합니다. 더 나아가 표준 모델에서의 보손-페르미온 상호작용 모델을, 진동자-큐비트 하이브리드 시스템을 통해 해밀토니안 시뮬레이션으로 구현하고자 하는 다양한 제안들도 활발히 이루어지고 있습니다.
특히 광학 네트워크와 달리 진동자-큐비트 하이브리드 시스템에서는 보손 계에 대한 비-가우시안 연산자를 더욱 효율적으로 구현할 수 있으므로, 보손이 포함된 복잡한 물리적 시스템도 한층 효과적으로 다룰 수 있게 됩니다. 이는 궁극적으로 양자화학이나 표준 모델은 물론, 다양한 과학 분야에서 다종 해밀토니안을 정확하고 효율적으로 시뮬레이션하는 데 큰 가능성을 열어줍니다.

이미지 확대보기

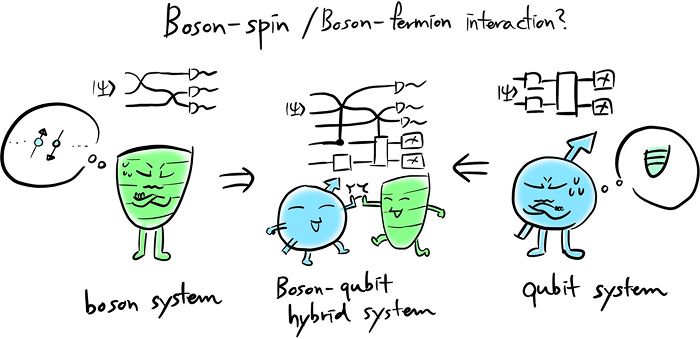
Figure 4.  보손과 큐비트간의 상호작용을 시뮬레이션 할 때에는 보손 또는 큐비트 하나의 시스템만 고려된 컴퓨터보다는 보손-큐비트 하이브리드 시스템(Boson-qubit hyrid system)에서 시뮬레이션하는 편이 효율적일 수 있다.

진동자-큐비트 하이브리드 시스템을 통해 해밀토니안 시뮬레이션을 수행할 때에도, 이 방식은 여전히 게이트 기반 양자 시스템이므로 큐비트 기반 양자 컴퓨터에서 해밀토니안 시뮬레이션을 위해 사용되던 여러 양자 알고리즘을 그대로 적용할 수 있습니다. 예를 들어, 복잡한 보손-스핀 혹은 보손-페르미온 시스템의 동역학을 분석하기 위해 해당 해밀토니안의 유니터리 연산자를 구현해야 한다면, 이를 진동자-큐비트 하이브리드 게이트로 이루어진 연산들의 곱으로 근사하는 스즈키-트로터 (Suzuki–Trotter)9 전개를 사용할 수 있습니다. 또한 유니터리 연산자의 선형 결합(LCU; Linear Combination of Unitaries), 양자 신호 처리(QSP; Quantum Signal Processing)10, 양자 특이값 변환(QSVT; Quantum Singular Value Transformation) 등과 같은 알고리즘 역시 적용 가능합니다.
이러한 양자 알고리즘은 원하는 양자 상태를 준비할 때도 활용할 수 있습니다. 예를 들어, 특정 해밀토니안과 초기 양자 상태가 주어졌을 때 에너지 고유 상태(주로 바닥 상태)를 만들고자 한다면, LCU·QSP·QSVT 등의 알고리즘을 통해 해당 초기 상태에서 목표 에너지 고유 상태만 남기도록 필터링 연산자를 구현할 수 있습니다.
마지막으로, 해밀토니안과 초기 상태가 주어졌을 때 그 상태가 갖는 특성을 파악하기 위해 다양한 관측량을 측정하는 일도 진동자-큐비트 하이브리드 시스템에서 가능합니다. 비록 이 시스템에서 보손을 직접 측정하는 방법은 아직 널리 알려져 있지 않지만, 보손이 가진 정보를 큐비트로 전달한 뒤 큐비트를 측정해 이를 대체할 수 있습니다. 이러한 측정 기법은 보손 연산자로 구성된 관측량뿐 아니라, 장(Field)과 보손 간 상호작용 등에 대한 관측량을 측정하는 방법도 포함합니다. 즉, 진동자-큐비트 하이브리드 시스템을 활용하면, 보손이 포함된 다양한 양자 시스템(보손-스핀, 보손-페르미온 등)에 존재하는 여러 관측량을 측정하고 추정할 수 있습니다.
정리하자면, 진동자-큐비트 하이브리드 시스템에서는 큐비트 기반 양자 컴퓨터에서 사용해 온 양자 알고리즘을 그대로 적용해 해밀토니안에 대한 유니터리 연산자를 생성하고 원하는 양자 상태를 준비할 수 있습니다. 또한 보손과 관련된 여러 관측량을 효과적으로 측정할 수 있는 방법이 제안되어 있어, 단일 종(스핀·보손·페르미온) 해밀토니안은 물론 보손이 포함된 다양한 종이 결합된 해밀토니안까지 효율적으로 시뮬레이션 할 수 있습니다. 이는 빛-물질 상호작용이나 핵-전자 상호작용을 다루는 해밀토니안을 보다 정확하고 빠르게 수행할 수 있게 하여, 화학 반응 및 재료 과학 등 실질적 응용 분야에 폭넓게 기여할 수 있을 것으로 기대됩니다.

이미지 확대보기

Figure 5.  큐비트 기반 컴퓨터, 보손기반 컴퓨터 각각 시뮬레이션가능한 모델들이 존재하고, 보손 큐비트 하이브리드 컴퓨터에서는 더 넓은 범위의 모델에 대해서 대처 가능하다.

진동자-큐비트 하이브리드 시스템은 해밀토니안 시뮬레이션뿐 아니라, 여러 양자 정보 분야에서 다양한 응용 가능성을 지니고 있습니다. 예를 들어, 보손 시스템을 활용한 GKP, 이항(Binomial), Cat 코드 등과 같은 오류 정정 코드를 하이브리드 시스템 내에 구현하거나, 이들 보손 기반 오류 정정 코드와 큐비트 기반 오류 정정 코드를 결합해 하이브리드 오류 정정 코드를 만드는 일도 가능합니다. 또한 큐비트의 이산적 정보 형태와 보손의 연속적 정보 형태 간 정보 변환을 통해 양자 정보를 처리하는 방식이나, 보손과 큐비트를 동시에 활용한 최적화 알고리즘 등은 기존의 큐비트 기반 양자 컴퓨터에서는 구현하기 어려웠던 분야이기도 합니다.
물론, 진동자-큐비트 하이브리드 시스템에서도 해결해야 할 과제들이 존재합니다. 예컨대 큐비트 기반 양자 컴퓨터에서는 연산자가 상한과 하한을 갖는 유계 연산자로 제한되지만, 보손 시스템에는 위치·운동량 연산자처럼 상한이 없는 무계 연산자들이 존재합니다. 이로 인해 큐비트 기반 양자 컴퓨터에서 사용되는 양자 알고리즘이나 해당 알고리즘의 분석 방법이 보손 시스템에는 그대로 적용하기 어려운 상황이 발생할 수 있습니다. 따라서 보손 시스템에 맞는 알고리즘과 그에 적합한 분석 방법을 마련해야 합니다.
또한 보손 역시 오류가 발생할 수 있으므로, 큐비트 기반 양자 컴퓨터에서 결함 허용 양자 컴퓨팅을 위해 오류 정정 코드가 필요한 것처럼, 보손을 위한 오류 정정 코드나 방법 역시 필수적입니다. 아직 이 분야에서는 활발한 연구가 이루어지지 않고 있습니다만, 이러한 문제들은 큐비트 기반 양자 컴퓨터가 보손을 포함하도록 확장되면서 새롭게 부각된 과제들이며, 이를 해결하는 과정은 양자 정보 분야 전반에 대한 우리의 이해를 한층 깊게 해줄 기회이기도 합니다.
종합해 보면, 하이브리드 시스템은 큐비트 기반 양자 컴퓨터에서 한 걸음 더 확장된 가능성을 제시합니다. 아직 연구 초기 단계에 머물러 있지만, 밝혀야 할 부분도 많고 응용 범위도 광범위하므로 앞으로 더욱 활발히 탐색되고 발전될 것으로 기대됩니다.

결론 및 향후 전망

본 열린강의실에서는 하이브리드 양자 컴퓨팅의 복합적 개념을 쉽게 이해할 수 있도록, 현재 이론 및 실험 동향을 간략히 살펴보았습니다. 진동자-큐비트 하이브리드 아키텍처는 이온 포획이나 초전도체 시스템 등 특정 플랫폼에서 이론적 모델 또는 초기 실험 단계로 연구되고 있지만, 앞으로 양자 시뮬레이션과 알고리즘 플랫폼으로서 크게 발전할 가능성을 지니고 있습니다. 하이브리드 양자 연속-이산 시스템은 막대한 잠재력을 갖추고 있어, 양자 컴퓨팅 기술 전반에 획기적인 진전을 가져올 뿐 아니라 물리·화학·재료 과학 분야의 다양한 문제를 해결할 중요한 기술적 기반으로도 기대됩니다. 특히 이러한 하이브리드 시스템의 개발은 결함 허용 양자 계산을 실현하기 위한 핵심 경로로 주목받고 있습니다. 이 같은 잠재력을 온전히 구현하기 위해서는 하이브리드 양자 연속-이산 패러다임에 대한 지속적이고 심층적인 연구와, 여러 분야의 연구자들 간 긴밀한 협력이 필수적입니다.

참고문헌연구

[Liu2024] Liu et al., Hybrid Oscillator-Qubit Quantum Processors: Instruction Set Architectures, Abstract Machine Models, and Applications, arXiv:2407.10381