quantum wave

• 저자 Google Quantum AI and Collaborators
• 저널 Nature 638, 920-926 (2025)
• 게재일 2024년 12월 09일
• DOI https://doi.org/10.1038/s41586-024-08449-y

Willow 칩과 실험 설계 - 105 큐비트에서 거리 7까지

양자컴퓨터는 양자 화학, 양자 시뮬레이션, 암호, 최적화 등 다양한 문제에서 고전컴퓨터와 비교해 계산우위를 가져올 것으로 전망됩니다. 이러한 계산 우위를 실제로 구현하기 위한 많은 노력이 계속되고 있으나, 현재 가장 큰 문제점은 양자 하드웨어에 발생하는 노이즈와 이로 인해 발생하는 계산 오류입니다. 소인수분해 및 양자 화학 문제와 같은 실용적인 문제 해결에 있어서 양자컴퓨터가 고전컴퓨터를 압도하려면 계산을 이루는 게이트 연산이 10-10수준의 오류율을 가져야 한다는 것이 정설입니다. 현실의 초전도, 이온 기반의 큐비트는 아직 10-3안팎에 머문닙다. 이 거대한 간극을 메우는 현실적인 유일한 방법이 양자 오류 정정(quantum error correction)입니다. 다만 이러한 노이즈가 있는 큐비트 기반의 성공적인 오류 정정은 개별 물리 큐비트(physical qubit)의 평균 오류율 가 코드의 임계값 보다 작을 때만 일어납니다.

또한 평균 오류율이 임계값보다 낮을 경우, 코드의 크기(코드 거리 d)를 증가시키는 방식을 통하여 논리 큐비트의 오류를 의 비율로 더욱 감소시킬 수 있습니다. 따라서 임계값 아래의 오류율을 달성하는 것이 성공적인 양자 오류 정정 코드 구현에 핵심입니다. 다양한 양자 오류 정정 코드 중 현재 가장 각광받고 있는 코드는 표면 코드(surface code)입니다 [그림 1a]. 표준적인 표면 코드는 2차원 격자 위에 많은 물리 큐비트를 논리 큐비트(logical qubit) 하나로 쌓아 오류를 실시간으로 감지하고 교정합니다. 양자 오류 정정 코드의 개별 임계값은 코드 및 하드웨어마다 다르지만, 표면 코드 기준으로 약 0.5% 내외로 알려져 있으며 매우 높은 임계값으로 여겨지기 때문에 특히 주목 받는 코드입니다.

  구글은 2022년 Natur에 출판된 논문 [Nature 614, 676–681 (2023)]에서 거리 3, 5 코드까지 확장해 코드를 크게 하면 논리 큐비트 오류율이 살짝 더 좋아진다는 힌트를 주며, 임계점 근처에 도달한 것을 확인하였습니다. 그러던 중 2024년 12월 9일 온라인 공개(2025년 2월 호 인쇄)된 새 Nature 논문이 결정적 전환점을 찍습니다. 제목 그대로 “Quantum error correction below the surface-code threshold”— 최초로 ‘임계선 아래’에 진입했음을 실험으로 입증한 것입니다.

이미지 확대보기

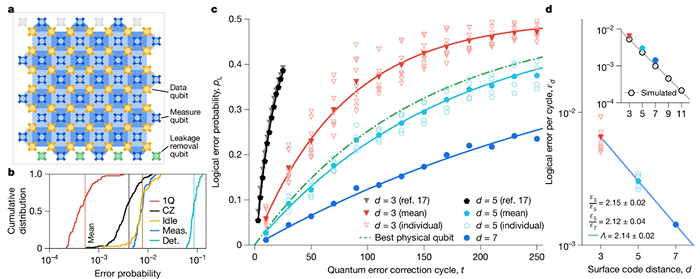
그림 1 a. 표면 코드, b. 연산 및 측정의 오류율, c. 서로 다른 크기의 표면 코드를 활용하였을 때 시간에 따른 논리 큐비트 오류율, d. 표면 코드의 크기에 따른 논리 큐비트 오류율

Willow 칩과 실험 설계 - 105 큐비트에서 거리 7까지

이번 연구의 주역은 ‘Willow’라 불리는 두 개의 초전도 프로세서로 이전까지 구글에서 사용한 Sycamore 초전도 프로세서에 비해 다양한 요소에서 향상된 성능을 자랑합니다. 하나는 72 큐비트(표면 코드 거리 5), 다른 하나는 105 큐비트(표면 코드 거리 7)다. 평균 결맞음 시간 T₁ ≈ 68 µs, 1-큐비트 게이트 오류율 < 0.1 %, 2-큐비트 CZ 게이트 오류율 < 1 %, 표면 코드 한 사이클은 1.1 µs만에 끝난다. 72 큐비트 칩에는 FPGA 기반 실시간 디코더가 붙어 있어, 측정 결과(신드롬)를 63 µs 만에 해석해 바로 다음 사이클에 반영합니다.
구글의 연구진은 Willow 프로세서에서 표면 코드를 구축하고, 먼저 각 데이터 큐비트를 표면 코드의 논리적 파울리 연산자 XL또는 ZL기저에 대응하는 상태로 준비하고, 이후 수십 ~ 수백 사이클동안 오류정정 루프를 돌립니다. 각 사이클에서는 측정 큐비트가 인접 데이터 큐비트의 패리티를 읽어오고, 누적된 신드롬을 디코더가 해석해 논리 오류를 추적합니다. 또한, 초전도 큐비트 특유의 ‘Leakage’(|2⟩ 준위로 빠져나감)는 전용 큐비트를 써서 매 사이클 빠르게 제거했습니다.

가장 중요한 결과로는 거리 5에서 거리 7로 확장했을 때 논리 오류율이 = 2.14 ± 0.02 배 감소하는 것을 규명했습니다. [그림 1d]. 이 는 이론식의 기울기와 일치하며, 임계선 아래로 진입했음을 가리킵니다. 또한 논리 큐비트 수명 291 µs이 최고 품질의 물리 큐비트 수명(119 µs)의 2.4 배가 된 것을 확인하였고, 이는 표면 코드를 사용하여 만든 논리 큐비트가 해당 논리 큐비트를 구성하는 물리 큐비트보다 더 좋은 성능을 보인다는 것을 의미하며, 이는 즉 ‘손익평형점 (breakeven)’(logical > best physical)을 넘었다는 것을 의미합니다. 이러한 지표는 “큐비트를 더 얹으면 더 좋아진다”는 교과서적 스케일링을 실험적으로 처음 검증한 값들입니다.

왜 중요한가 - ‘될까?’에서 ‘얼마나 크게?’로

해당 논문의 가장 중요한 결과는 임계선 최초로 돌파했다는 것입니다. 표면 코드를 만든 이후 25년 만에, 물리 오류율을 완전히 임계선 밑으로 낮춘 사례가 등장했습니다. 이제 양자 오류 정정의 성공 가능성은 가설이 아니라 실측 데이터가 되었습니다. 또한 실시간으로 양자 오류 정정을 완성한 하드웨어라는 것이 중요합니다. 일반적으로 신드롬 측정 결과를 처리하는 과정 또한 계산 복잡도 관점에서 어려운 과정으로 알려져 있으며, 따라서 실시간으로 오류 정정하는 것에 어려움을 주는 과정인데, 본 실험에서는 하드웨어, 디코더. 누설 제거까지 하나의 패키지로 실시간으로 작동했다는 점이 특히 중요합니다. 이전 결과는 후처리 디코딩에 많이 의존했고, 실시간 폐루프에서는 잡음 누적으로 다시 무너지곤 했습니다.

남은 숙제 — 계산이 아닌 ‘메모리’였다는 점

이번 논문은 어디까지나 “거리 7 양자 메모리”실험이다. 실제 양자컴퓨터를 구현하기 위해서는 양자 메모리를 넘어서 해당 프로세서에 논리 게이트를 적용하는 것이 필수적입니다. 오류를 억제한 상태로 논리 게이트(CNOT, T 등)를 실행하려면 추가 보호 계층이 필요합니다. 또한 2개의 표면 코드 사이에 논리 2-큐비트 게이트를 구현하는 것은 본 논문에서 구현한 메모리를 넘어서 격자 수술 (lattice surgery) 기법 등이 필수적이고, 이를 실제 실험으로 구현하는 것은 양자메모리를 넘어 양자컴퓨팅을 구현하는 것에 중요한 과제가 될 것입니다.

또한 시간당 한 번꼴로 등장하는 고에너지 상관 오류가 발견되었는데, 이 희귀 사건이 장거리 코드에서 ‘바닥’(floor)을 만든다. 재료 결함, 우주선, 2형 접합 등 뿌리가 복잡해 근본 대책이 필요합니다.

한편 디코더 속도도 문제 입니다. 거리 11 ~ 17로 키우면 신드롬 데이터가 폭증하므로, 맞춤형 ASIC 가속기나 병렬 GPU 해법이 필수 입니다. 마지막으로, 표면 코드 외에 LDPC, Color Code, Floquet Code같은 대안 코드가 실제 칩에 얹힐 수 있을지, 연구실마다 경쟁이 뜨거워질 전망입니다.

정리 — 임계선 돌파 이후의 과제

Willow 실험의 중요한 골자는 양자 오류 정정 이론이 제시한 ‘극단적으로 완벽한 큐비트’를 찾기보다는 ‘적당히 좋은 큐비트를 대규모로 조직화한 아키텍처를 구성하는 것이 현실적 해법이라는 것을 실제 하드웨어적으로 구현하고 검증한 것입니다. 이제 양자 오류 정정은 이론적인 제안을 넘어 실제 하드웨어적인 양자컴퓨팅을 실현하는 것이 가능하다는 것을 암시합니다. 물론 양자 오류 정정의 실효성을 검증한 것은 사실이나, 실제 양자컴퓨터로의 활용에 있어서 계속하여 하드웨어 및 소프트웨어적인 성능 개선이 필수적이다. 양자 오류 정정은 단일 요소의 성능 개선을 넘어, 하드웨어, 제어 전자, 디코더, 컴파일러, 코드 설계가 동시에 진화해야 하는 다학제적 공학 과제라고 볼 수 있습니다. 재료 잡음과 희귀 상관 오류를 줄이는 공정 고도화, 오류 인식을 전제로 한 컴파일러와 동적 스케줄링, 더 빠른 디코더와 LDPC, Floquet 같은 새로운 코드 구조의 탐색까지 모든 층위가 맞물려야만 대규모, 오류 정정된 양자컴퓨터가 현실이 될 것입니다.

연구 그룹 소개 및 연구 전망

Google Quantum AI연구팀은 초전도 큐비트 기반의 양자 프로세서 개발의 세계적인 선도 그룹으로, 대표적인 업적으로는 2019년에는 53개의 초전도 큐비트 기반의 Sycamore 프로세서를 통해서 무작위 회로 샘플링을 구현하여 최초의 양자 계산 우위를 주장한 것이 있으며, 최근에는 본 기사에서 주로 다룬 Willow 프로세서를 통해서 양자 오류 정정을 시연하여 오류를 허용하는 범용성 양자 컴퓨터의 시대로 가는 중요한 실험을 성공하였습니다.